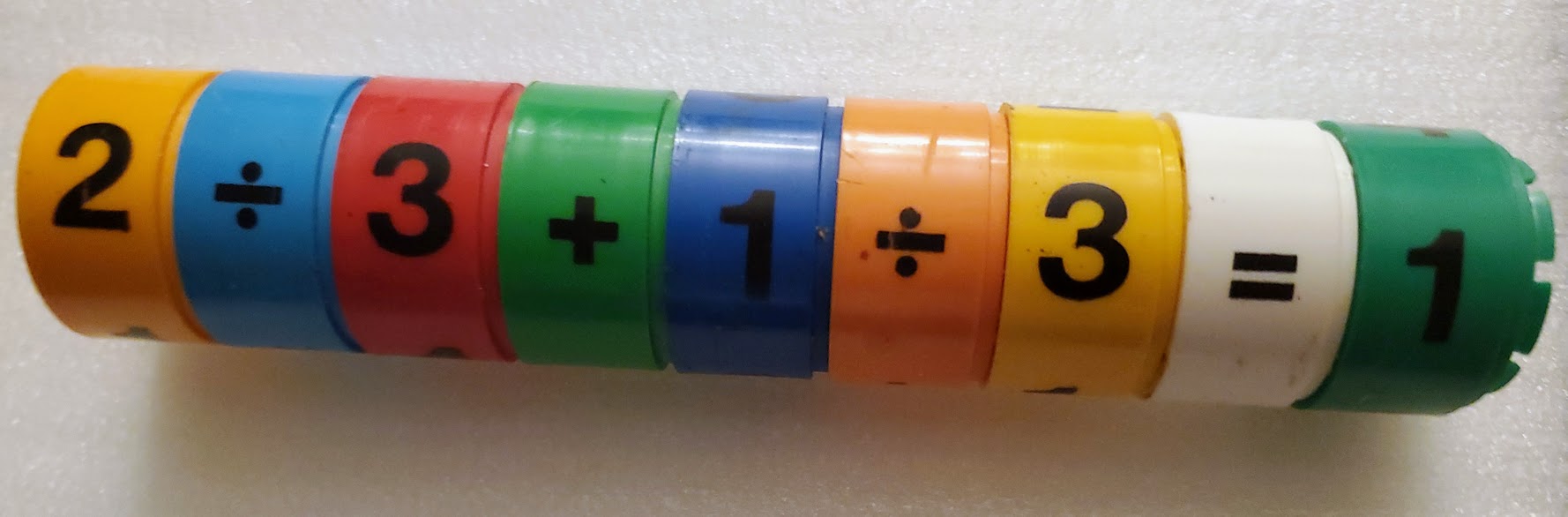Many years ago, when I was still a teenager, I got this puzzle as a gift. It consistes of 9 plastic rings that can be placed together in any order and rotated 4 divfferent ways. The objective is to make it so that, when completed, all 4 equations that are formed balance out (for example, 2-1+3-1=2).

Definitely a tough puzzle, there are:

• 5! (120) ways to arrange order the number rings,
• 2x3! (12) ways to order the operations (Note that there are 4 places that the = can go, but the solution is symmetrical since you can swap the two sides of the equation)
• 4⁷ (16384) ways to rotate the rings in each ordering.

The frustrating part of it is that when you find a single side that works, you're really no closer to a solution than you were when you started if the other sides don't work. And there's really no systematic way to try all the combinations and rotations to look for a solution.

Or, is there? That's where the CompSci degree comes in. Can a program be written to find the solution?

Turns out it can.

The biggest surprise here is that there are multiple solutions! However, there are 3 of them with the "=" between two complex operations (probably not intended as a solution), and one solution which involves the addition of 2 fractions, also probably unintended. I have ordered the array rings such that the intended solution displays first.

Footnote: Through a Google search, I found that the name of this puzzle is "Digi Disc" and that are a variety of sizes and configurations. If I ever get another one of them, I may generalize this algorithm for the additional solves.